Strassenのアルゴリズム
行列の積を求めるアルゴリズムに、シュトラッセンのアルゴリズムと言うのがあるそうだ。
シュトラッセンのアルゴリズム - Wikipedia
Strassen algorithm - Wikipedia
Part II: The Strassen algorithm in Python, Java and C++ · Martin Thoma
まあ、wikipediaによると単純な3重ループより計算量が少し小さくなるらしい。
実装自体はそんなに難しくなさそうなので、scalaで書いてみた。
main関数は特に意味はない。テストのときはこれをimportして使った。
部分行列をどこまで分割していくかで結構性能が変わる。上の記事では一番小さい部分行列をleafと呼んでいたのでそれにならってここでもそのように表記する。
ためしに1024*1024の零行列同士の積を、leafの値を変えて計算し、かかった時間をグラフにした。
ちなみに使用したマシンは、数年前は新しかったiMac。
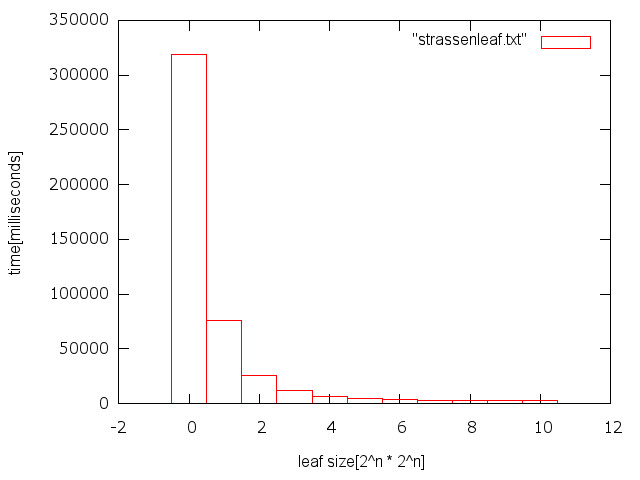
データはこちら。
| leafのサイズ[2^n * 2^n] | 時間[ミリ秒] |
| 0 | 318759 |
| 1 | 75572 |
| 2 | 25543 |
| 3 | 11921 |
| 4 | 6901 |
| 5 | 4567 |
| 6 | 3469 |
| 7 | 2956 |
| 8 | 2722 |
| 9 | 2737 |
| 10 | 3222 |
このマシンでは、leafの値は256ぐらいがよさそうだ。
ということで、どれくらい速くなるのかを
の3つで、計算時間を比較した。
で、得られた結果をグラフにまとめたのがこちら。赤がシュトラッセン、青がijk、緑がikjとなっている。
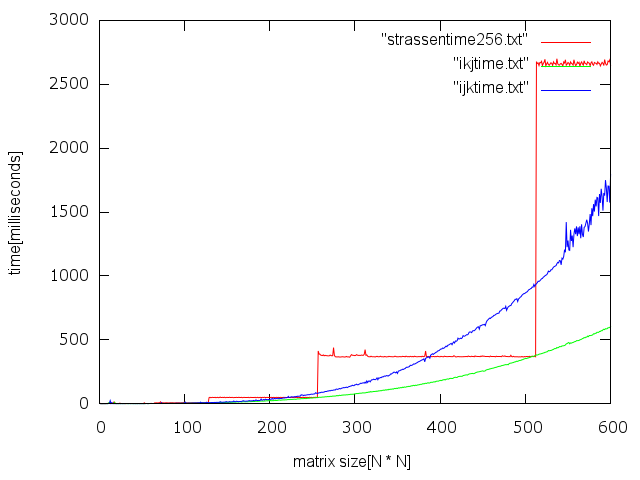
ちょっとわかりにくいので行列のサイズが512のときのデータを示す。
| アルゴリズム | 時間[ミリ秒] |
| ijk | 932 |
| ikj | 377 |
| Strassen | 368 |
シュトラッセン、あまり速くなさそうに見える。
ループの順番変えるだけでこんなに性能良くなるのには驚いた。
シュトラッセンのアルゴリズムは、行列を次に大きい2^nの正方行列に拡大して計算するので、平べったい感じのグラフになる。なので、行列のサイズが130とか520とかだと、とても効率がよろしくないことになる。
ikjの方が色々な行列に対応できるので、扱う行列が2^nに近いものでなければ、こっちの方がいい感じなのかもしれない。
……なーんか腑に落ちないので、試しに大きめの正方行列でikjとシュトラッセンの時間を計ってみた。
| 行列のサイズ[N * N] | ikj[ミリ秒] | シュトラッセン[ミリ秒] |
| 1024 | 3354 | 3121 |
| 2048 | 25765 | 21154 |
何回か計ってみたが、大体こんな感じになった。
この表を見ると、シュトラッセンの方が速いことが分かる。
大きい行列かつサイズが2^nに近いものであれば、シュトラッセンのアルゴリズムは威力を発揮しそうだ。